トレーニーとしてどのくらいの重量を挙げられればすごいのかというのは、本質的に主観的な判断になりがちなテーマです。客観的に答えを出すために一般的に使われる方法はいくつかありますが、それぞれに問題を抱えています。この記事では、ほとんど知られていないものの挙上重量を正確に比較することができる方法を紹介したいと思います。
絶対重量 vs 相対重量
まずは、絶対重量と相対重量の違いについて確認しておきましょう。
絶対重量は、体重に関係なくどれだけの重量を挙げることができるかということです。例えば、次の条件の2人を比べるとします。
- トレーニーA:体重65kgでベンチプレスが150kg挙がる
- トレーニーB:体重130kgでベンチプレスが152.5kg挙がる
この場合、トレーニーBの方が絶対重量は大きいということになります。しかし、トレーニーAの方が体重に対する挙上重量が大きく、相対重量が大きいということになります。
絶対重量はとにかくどれだけ大きな重量を挙げられるかということなので、この上なくシンプルです。対して、相対重量をどう評価するのが最善かというのは、多くの人が考えるほどシンプルではありません。
体重比で考える方法
相対重量を考えるのに、最も広く使われるのが体重比で考える方法です。例えば、スクワットで体重 × 2倍を目指すという感じです。「上級者」の目安として次のような数字が使われるのをよく見かけます。
- スクワット:体重 × 2
- ベンチプレス:体重 × 1.5
- デッドリフト:体重 × 2.5
上級者のさらに上にあたる「エリート」として次のような数字が使われることもあります。
- スクワット:体重 × 2.5
- ベンチプレス:体重 × 2
- デッドリフト:体重 × 3
こういう計算方法には大きな問題が2つあります。
体重比を使う問題1:身体の大きな人に厳しい
例えば、体重70kgでデッドリフトが210kg挙がるとすると、それは非常に強いと言えますが、ありえないことではまったくありません。しかし、体重140kgになると、体重の3倍は420kgになります。420kgのデッドリフトとは、世界でこれまでに達成した人が100人もいないような数字です。
下の表はパワーリフティングの世界記録を体重の階級ごとにリスト化したものです。
| 表1:体重比で見る世界記録(ニーラップ有り) | ||||||||
|---|---|---|---|---|---|---|---|---|
| 階級 | スクワット | ベンチプレス | デッドリフト | 合計 | ||||
| 重量 | 体重比 | 重量 | 体重比 | 重量 | 体重比 | 重量 | 体重比 | |
| 123 | 639 | 5.2 | 455 | 3.7 | 634 | 5.15 | 1339 | 10.89 |
| 132 | 565 | 4.28 | 4.62 | 3.5 | 628 | 4.76 | 1471 | 11.14 |
| 148 | 611 | 4.13 | 498 | 3.36 | 697 | 4.71 | 1581 | 10.68 |
| 165 | 710 | 4.3 | 529 | 3.21 | 717 | 4.35 | 1714 | 10.39 |
| 181 | 744 | 4.11 | 556 | 3.07 | 791 | 4.37 | 1840 | 10.17 |
| 198 | 810 | 4.09 | 565 | 2.85 | 870 | 4.39 | 2028 | 10.24 |
| 220 | 915 | 4.16 | 586 | 2.66 | 901 | 4.1 | 2110 | 9.59 |
| 242 | 881 | 3.64 | 661 | 2.73 | 893 | 3.69 | 2210 | 9.13 |
| 275 | 992 | 3.61 | 675 | 2.45 | 906 | 3.29 | 2380 | 8.65 |
| 308 | 1030 | 3.34 | 701 | 2.28 | 939 | 3.05 | 2425 | 7.87 |
| 重量単位:lbs | ||||||||
ほとんどの場合で階級が上がるごとに、体重に対する挙上重量の倍率は下がっていくことが分かります。
最軽量の階級では、デッドリフトで体重の5倍以上の記録が出ていますが、重量級はおろか中量級でもこんな数字は期待できません。ベンチプレスでは、重量級や中量級の選手が体重の3.5倍を挙げるのも現実的ではないでしょう。
体重に対する倍率は階級が上がるごとに小さくなっていますが、この表の数字はすべて世界記録なので、すべてがとんでもなくすごい数字のはずです。つまり、幅広い体重の人の挙上重量を比較するのに、体重比を使うのは良い方法ではないということです。もし、この方法が有効なのであれば、世界記録を出したパワーリフターの体重と挙上重量の比率は、階級が違っても近い数字になるはずです。
体重比を使う問題2:生物学的におかしい
体重に倍率を掛けて挙上重量を計算する方法は、生物学的に見たヒトの身体と噛み合わないのでうまくいきません。生物学的にと言うと大層に聞こえますが、理論的にも現実の世界でも確実に言えることです。
相対成長スケーリング
相対成長スケーリングとは、特定の種の生物や、異なる種の生物の大きさが変わるのに合わせて起こる変化のことを言います。相対成長スケーリングは、あらゆる場面に応用されていますが、身体の大きさと代謝率に関するものがおもしろいので紹介します。
いろんな生き物の代謝率
マウスからクジラにいたるまで大きさの異なる生物の身体のサイズと代謝率をグラフ化して比べると、ほぼ完全に直線上に並ぶ関連性が見られます。この時の直線の傾斜は3/4になり、これをクライバーの法則と呼びます。
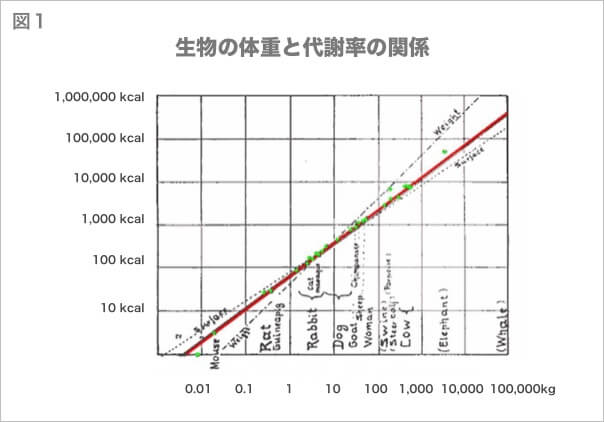
クライバーの法則は1947年に初めて発見されました。その後、この身体の大きさと代謝率の関係は、バクテリア、ミトコンドリア、呼吸複合体といったマウスよりも小さなものにも当てはまることが発見されました。単細胞生物、冷血動物、温血動物などに合わせて若干の修正は加えられたものの(これらの生物すべてで基本的に同じ関連性が確認されていますが、趨勢線の傾きは3/4から少しズレます。)、70年を経たいまも相対成長スケーリングの根本的な関連性は揺るがず支持されています。
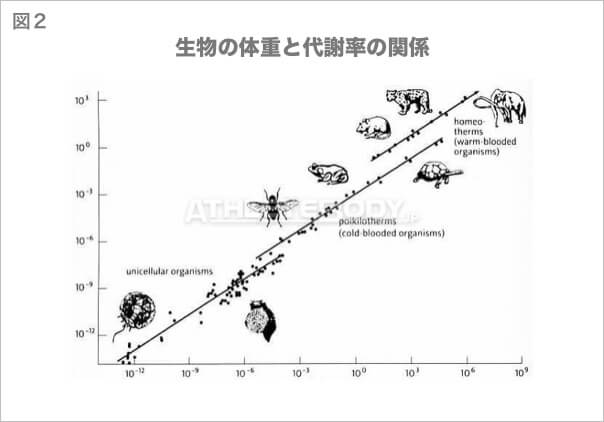
もう少し実感しやすい例で考えてみましょう。
体重30gのマウスの基礎代謝は5kcal程度になります。体重6gあたり1kcalという計算になります。とても小さく感じるかもしれません。ヒトの場合、体重が70kgであれば基礎代謝は1600kcal程度になります。これは、体重44gあたり1kcalという計算になります。つまり、体重に対する基礎代謝は、ヒトよりもマウスの方が7〜8倍大きいということになります。
いろんな生き物の力の強さ
身体の大きさと力の強さの間にも似たような関係があります。例えば、アリとHafþór Björnssonという世界で3本の指に入る超重量級のストロングマンを比べてみましょう。
アリは自分の体重の20倍くらいの物を長距離運ぶというようなことを絶えず行っています。モデリング研究では、理論上アリは自分の体重の5000倍くらいまでの重さを持てるという見積りが出ています。それ以上になると、アリの身体で最も弱い首が折れてしまうということです。
一方、ストロングマンのBjörnsson選手は、2015年に自分の体重の3.5倍になる640kgのログを持って5歩歩いたことで人々をあっと言わせました。
ヒトの身体がどれだけの重量に絶えられるのかを実際に実験することはできないので具体的な数字は分かりませんが、350,000kg(70kg × 5000倍)には遠く及ばないでしょう。
相対成長スケーリングと相対筋力
相対成長スケーリングは相対筋力にも当てはめることができます。その背景には、ヒトの身体の大きさが変わると、それに合わせて一定の比率で変化するものが2つあります。
ひとつ目は、筋肉が収縮することで生み出される力の大きさです。これは筋断面積とほぼ完全に1:1の関係にあります。筋断面積は平方数でcm²単位で測定します。
ふたつ目は体重です。体重は身体の体積と関連があります。ほとんどの人は身体の密度が大きく変わらないので、身体の体積が大きくなると体重が増えることに直結します。身体の体積は立方数でcm³単位で測定します。
少し話が逸れてしまいますが、密度について補足しておきます。
下のような画像をあちこちで見かけます。「体脂肪よりも筋肉の方が密度が高いから、体脂肪を落として筋肉を付ければ同じ体重でも身体はグッと小さくなるよ!」というメッセージを伝えるために使われることが多いです。

この画像に関してはデタラメもいいところです。筋肉の密度は約1.06kg/Lで、体脂肪の密度は約0.9kg/Lです。つまり筋肉の方が密度が高いというのは間違いありませんが、その差は15%程度でこの画像に関してはデタラメもいいところです。下の画像の方が実際に近いでしょう。

体脂肪測定に使われる水中体重測定やBod Podでは、体脂肪と筋肉の密度の差を計算に入れて測定値が出されます。15%というのは、ある程度の精度を持って体脂肪測定ができるだけの差だとは言えます。ただ、一部の人が考えるように上の画像ほどの差があるわけではなく、体脂肪量に非常に大きな差が無ければ、身体の体積は大きく変わりません。
体形改善という意味では、同じ体重で筋肉が多く体脂肪が少なくなればセクシーになる人が多いでしょう。しかし、それは体組織の密度に大きな差があるからではないということです。
相対成長スケーリングに話を戻します。体脂肪率が変わらず筋肉が増えた場合、体重は筋力よりも速いペースで増えていくはずです。これは、身体が大きくなって各部の長さが2倍になれば、筋力は4倍(2²)になり、体重は8倍(2³)になるはずだという計算です。身体の体積と筋力の推移をグラフ化すると、上の代謝率のグラフのように直線的な関係が見られるはずです。ただ、趨勢線の角度は3/4ではなく2/3になるはずだと考えられます。
この関係を踏まえて、「筋力×体重-2/3」という方程式で相対筋力の高さを比べることができます。試しに、体重60kgで120kgのスクワットと体重90kgで170kgのスクワットのどちらが相対筋力が高いかを計算してみると、相対成長スケーリングのスコアは前者が10.19で、後者は11.01になります。先に話したように、相対成長スケーリングでは、生物学的にヒトの身体がどうできているかを踏まえた計算ができます。そして、体重60kgで120kgは体重の2倍、体重90kgで170kgは体重の1.89倍にしかなりませんが、相対成長スケーリングで見た相対筋力は、後者の方が高いということになります。
ここまでの話は、勝手な理屈を並べているだけに見える人もいるかもしれませんが、研究の世界では筋力パフォーマンスを比較するのに最善の方法としてほぼ見解が一致しています。実際に、高レベルのアメリカンフットボール選手をはじめ、いろんなタイプの被験者でその妥当性が認められています。
そんなのピンと来ないという人には、下の表2を見て、体重比を出した表1と比べてみてください。
| 表2:相対成長スケーリングで見る世界記録(ニーラップ有り) | ||||||||
|---|---|---|---|---|---|---|---|---|
| 階級 | スクワット | ベンチプレス | デッドリフト | 合計 | ||||
| 重量 | スコア | 重量 | スコア | 重量 | スコア | 重量 | スコア | |
| 123 | 639 | 25.84 | 455 | 18.4 | 634 | 25.63 | 1339 | 54.14 |
| 132 | 565 | 21.79 | 4.62 | 17.82 | 628 | 24.22 | 1471 | 56.74 |
| 148 | 611 | 21.84 | 498 | 17.8 | 697 | 24.91 | 1581 | 56.51 |
| 165 | 710 | 23.6 | 529 | 17.58 | 717 | 23.83 | 1714 | 56.98 |
| 181 | 744 | 23.25 | 556 | 17.38 | 791 | 24.72 | 1840 | 57.5 |
| 198 | 810 | 23.84 | 565 | 16.63 | 870 | 25.61 | 2028 | 59.7 |
| 220 | 915 | 25.11 | 586 | 16.08 | 901 | 24.72 | 2110 | 57.9 |
| 242 | 881 | 22.69 | 661 | 17.02 | 893 | 23 | 2210 | 56.91 |
| 275 | 992 | 23.46 | 675 | 15.96 | 906 | 21.42 | 2380 | 56.28 |
| 308 | 1030 | 22.58 | 701 | 15.37 | 939 | 20.59 | 2425 | 53.17 |
| 重量単位:lbs | ||||||||
相対成長スケーリングを使うと、すべての階級をずっと平等に比較できるのが分かると思います。
スクワットでは、突出して大きい数字が2つあります。
- 体重123lbsで638lbsを挙げたStanaszek選手(この人は体重114lbsで617lbsも挙げています。)
- 体重220lbsで915lbを挙げたSam Byrd選手
ベンチプレスでは、軽量級のスコアが少し高い傾向が見られます。これは、軽量級4階級の世界記録はパラリンピック選手によって樹立されたものだということが影響していると考えられます。パラリンピック選手はベンチプレスで下半身の力を使うことができませんが、同じ体重の一般選手よりも上半身の筋量をずっと大きくできるので、その階級の中で戦う上で有利になります。(これは、Stanaszek選手の小人症がスクワットに有利に働くことや、Gant選手の脊椎側湾症がデッドリフトで有利に働くことに似ています。)例えば、Lei Liu選手は体重148lbsで498lbsを挙げ、それまでの世界記録を58lbs更新しています。こういったパラリンピック選手を除くと、スコアは16〜17.4の範囲にかたまっています。ハッキリと外れているのは、308lbsで701lbsという記録だけです。
デッドリフトでは、Lamar Gant選手の123lbsで634lbsという記録がぶっちぎりかと思いましたが、Belyaev選手の198lbsで870lbsもそれに肉薄しています。Konstantinov選手の275lbsと308lbsでの強烈なデッドリフトは、少しスコアが低く出ています。デッドリフトに関しては、相対成長スケーリングは重量級選手に少し不利な数字を出すのかもしれません。
トータルを見ると、特定の階級に有利だったり不利だったりする傾向は見られません。全体としてはスコア56〜58の範囲にかたまっており、123lbs級と308lbs級だけが少し後れをとっている形です。198lbs級で2028lbsを挙げたErnie Lilliebridgeが唯一抜きん出ています。
ノーギアの世界記録でも基本的には同じ傾向が見られます。
| 表3:相対成長スケーリングで見る世界記録 | ||||||||
|---|---|---|---|---|---|---|---|---|
| 階級 | スクワット | ベンチプレス | デッドリフト | 合計 | ||||
| 重量 | スコア | 重量 | スコア | 重量 | スコア | 重量 | スコア | |
| 59 | 226 | 14.91 | 170 | 11.22 | 270.5 | 17.85 | 661 | 43.61 |
| 66 | 240.5 | 14.73 | 182.5 | 11.17 | 278 | 17.02 | 653.5 | 40.01 |
| 74 | 260 | 14.75 | 210.5 | 11.94 | 310.5 | 17.62 | 712.5 | 40.42 |
| 83 | 280.5 | 14.74 | 205 | 10.77 | 316 | 16.61 | 783.5 | 41.18 |
| 93 | 303 | 14.76 | 232.5 | 11.33 | 372.5 | 18.15 | 847.5 | 41.29 |
| 105 | 330 | 14.83 | 221.5 | 9.95 | 343 | 15.41 | 867.5 | 38.98 |
| 120 | 375 | 15.41 | 235 | 9.66 | 37.15 | 15.27 | 945 | 38.84 |
| 重量単位:kg | ||||||||
ここでも、どこかの階級にハッキリ有利だったり不利だったりする傾向は見られません。
スクワットでは、120kg級Mohamed Bouafla選手の375kgが頭ひとつ抜け出している以外、ほぼ横一線です。
ベンチプレスは、軽量級の方が大きなスコアが出ているようにも見えます。ただ、IPFが階級を再設定した以降に、105kg級と120kg級で本当に大きな記録が出ていないだけとも考えられます。Dennis Gieri選手が93kg級で232.5kgを挙げられるのなら、今後105kg級や120kg級の選手が現在の221.5kgと235kgの世界記録を更新するのは十分期待できるでしょう。ちなみに、Geri選手は93kg級で237.5kgも成功させています。ただ、IPFの世界記録として認められる大会でなかったので記録に反映されていません。
デッドリフトに関しては、ここでも軽量級に少し有利なように見えます。ただ、Krzysztof選手が93kg級で372.5kgを挙げているのを見ると、ベンチプレスと同じように重量級の記録はこれから伸びて来るのではという見方もできます。
トータルでは、特定の階級に有利だったり不利だったりする傾向は見えません。59kg級Sergey Fedosienko選手の661kgというのが突出している以外は38.9〜41.3の範囲にかたまっています。
相対成長スケーリングは、理論的にはしっかりしていますが、すべての階級をまたいだパワーリフティングの記録を比較するのに実際に使えると言えそうです。強いて言うと重量級の選手のデッドリフトについては、少し不利に働く可能性はあるかもしれないというくらいです。
ただ、相対成長スケーリングでは、うまく対応できない問題がひとつあります。
最重量級はどうなる?
相対成長スケーリングが相対筋力の比較に役立つのは、体重(身体の体積)と力の強さ(筋断面積)が強く結びついているからです。この2つの要素が関連性が維持されて、理論上の想定から大きくズレない率で伸びていけば、異なる階級の挙上成績を正確に比べることができます。
しかし、体脂肪率が大きく変わると、体重と力の強さの関係が大きく崩れることになります。軽量級から中量級のトップ選手の体脂肪率は、ほとんどの場合、10〜15%程度の範囲に収まり大きな違いはありません。ドラッグフリーの105kg級や120kg級の重量級でも、体脂肪率が高くなりすぎない範囲に抑えている選手もいます。しかし、体重制限のない最重量級になると、絞れた身体の選手を見ることはありません。そして、それは相対成長スケーリングのスコアに表れています。
例えば、Ray Willams選手の体重171.65kgで425.5kgを挙げたスクワットはすごいですが、相対成長スケーリングのスコアは13.78になります。他の7階級のスクワットのスコアの平均は14.88なので、Ray Willams選手のスコアは平均を6.5%下回るということになります。Benedict Magnusson選手が体重173kgで460kgを挙げたデッドリフトもすごいですが、相対成長スケーリングのスコアは19.31で、他の10階級の平均23.87を大きく下回ります。
なんとか最重量級の選手も同じ土俵に立たせて比べたくなるところです。
全階級を平等に比較するには?
これまでパワーリフティングやウェイトリフティングでの挙上成績を比べる方程式は、この問題を克服するべく開発されてきました。
パワーリフティングでは、これまでに複数の方程式が使われてきました。
最初は、Schwarz/Malone式が採用されました。これは1970年代に当時スポーツとして誕生間もないパワーリフティングのトップ選手の成績を基に開発されました。
1990年代半ばには、方程式を更新するべきだという声が高まり、当時のトップ選手のデータを基にWilks式が開発されました。
2000年代半ばには、Schwarz/Malone式は軽量級に有利な反面、Wilks式は重量級に有利になっているという声があがります。そこで、実質的に両者の間を取る形でGlossbrenner式が開発されました。
その他にも複数の方程式が出てきましたが、結局はWilks式とGlossbrenner式に取って代わられる形になりました。現在でも、Wilks式がIPFやその関連競技団体で使われており、最も一般に浸透しているので、Wilks式についてもう少し掘り下げてみます。
Wilks式の問題点
Wilks式は、1987年〜1994年までのIPFのさまざまな大会における競技成績から、各階級の世界レベルの選手が挙上可能であると考えられる重量と体重(各階級の制限体重)との関連性を反映した5次の多項式に基づいています。(引用元)
中量級に不利になる
Wilks式は、方程式の開発の過程に大きな問題点があります。
Wilks式の開発にあたって、多くの競技大会での挙上成績、それも各階級に複数のハイレベルな選手がいる大会での成績が使われました。これは、Wilks式の強みのように聞こえるかもしれませんが、実は大きな欠点につながっています。
大会に出場する選手の大半は一般的な体格で、中量級の階級には軽量級や重量級の2倍くらいの選手が集まります。それだけ選手層の厚みがあると、力のある選手が集まる確率が高くなります。体重65kg〜90kgくらいの範囲の階級でトップ10入りする選手と、その範囲より軽い階級や重い階級でトップ10入りする選手を比べると、前者の方が才能ある選手が多くなるということです。
例えば、軽量級と重量級には、「トップ5」に入る才能を持った選手が5人いるとします。「トップ10」に入る選手は10人、「トップ20」に入る選手は20人としましょう。それに対して、全体の選手層が2倍になる中量級の階級では、同じ力を持った選手が2倍いると考えられるので、「トップ5並み」の才能を持った選手は10人、「トップ10並み」の選手は20人、「トップ20並み」の選手は40人いると推定できます。

これを踏まえて、各階級でトップレベルにいる複数の選手の挙上成績を基に方程式を作ると、中量級に厳しい数字を出すことになります。例えば、方程式が各階級の上位10人の挙上成績を基に作られたとすると、軽量級と重量級では、「トップ5」の力を持った選手が5人と、残り5人には「トップ10」の力を持った選手が入ると考えられます。しかし、中量級の上位10人は「トップ5並み」の力を持った選手で埋め尽くされます。中量級には軽量級や重量級よりも才能ある選手が多くなるので、レベルの高い挙上成績を基準にスコアが計算されてしまうということです。

相対成長スケーリングのスコアをWilksスコアに比較してみると、このことが浮き彫りになります。まず、相対成長スケーリングでは、相対筋力を正確に比較することができます。そこで、各階級で相対成長スケーリングのスコアが同じになる挙上重量で、Wilksスコアがどう変化するかを比べます。
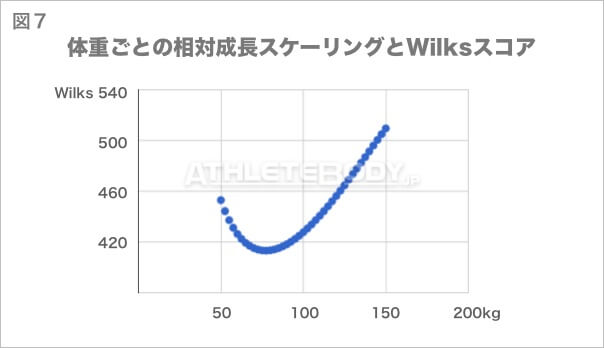
グラフの曲線が真ん中付近で落ち込んでいるのがハッキリ分かります。曲線の一番低くなった位置は、体重77.21kgでした。(Wilksスコアが最も低く出る体重)体重65kg〜92.5kgの範囲に入る男性にとって、Wilksスコアは不利に働きます。女性の場合は、曲線の最も低い位置が71.87kgになりました。
Wilks式は重量級に有利に働くと言われてきたことは的外れではなかったようです。例えば、体脂肪をあまり増やさず、110kg級で非常に高いレベルのパフォーマンスが出せれば、70kg〜75kgくらいの階級の選手よりも、Wilksスコアは6.7%大きく出るという計算になります。この差は125kg級になると、12.5%まで広がります。体重60kg以下の軽量級はここまで極端ではないものの、やはり中量級よりもWiksスコアは有利になります。
Wilks式の開発では、各階級を平等に扱うために複数のトップ選手のデータを用いたのですが、実際には65kg〜92.5kgの範囲に力のある選手が集中しているので、この範囲に当てはまる選手に不利が方程式ができあがってしまったということです。同じWilksスコアを得るためには、軽量級(60kg以下)や重量級(100kg以上)の選手よりも相対筋力を上げなければいけないということになります。
ギア無しとギア有りの記録が混ぜて使われている
1992年にIPFではリフティングギアの使用を認めるようになりました。Wilks式は1987年〜1994年の記録に基づいて開発されたので、ギア無しでの挙上記録と、当時出はじめたスクワットスーツやベンチシャツを使った挙上記録が混ざっていることになります。
こういったギア使用は、現在のギア無しの大会では認められていません。使用不可能なギアを使った挙上記録が開発段階で部分的に取り入れられているにもかかわらず、ギア無しの大会でWilks式が使われています。さらに、Wilks式はギア有りの大会でも使われています。Wilks式の開発に使われたデータはギア無しの挙上記録の割合の方が大きかった上に、1992年当時にあったギアと現在のスクワットスーツ、ベンチシャツ、ニーラップの性能は比べ物になりません。
過剰適合
過剰適合とはデータをモデル化する際に、本来の関連性を見るのに重要でないものまで過剰に考慮してしまうことを指す言葉です。これは実際のパワーリフティングよりも理論上の問題なのですが、Wilks式について注意しておくべきことです。
ここでは、筋力と体重というたった2つの要素の関連性を見たいということです。この2つの要素の関係が予測不可能な変化をするわけでなければ、5次の多項式のように複雑な方法を採る必要はないはずです。方程式を作る際に指数を増やしていけば、データに噛み合うようにすることはできますが、Wilks式のような方程式をつくる目的はデータに合わせることではなく、データから筋力と体重の間にある関連性を導き出すことです。
十分なデータがない状態で必要以上に複雑なモデルを作ろうとする過剰適合は、絶対避けなければいけないことです。
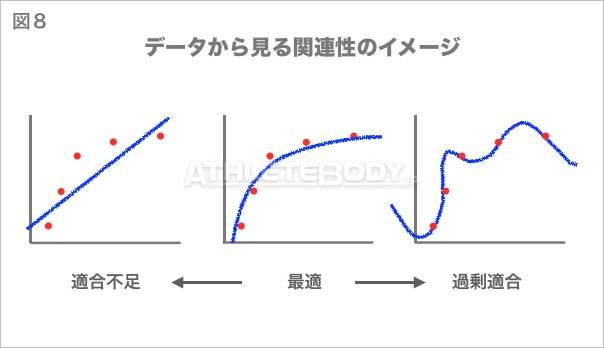
Wilks式では過剰適合を起こしているわけではありません。しかし、データから関連性を導き出そうとするのではなく、データそのものが関連性を示していると捉えてしまっているように見えます。
Edwin Hubbleという人が、このことを見事に表現してくれているので紹介します。
v = H₀D
この方程式は物体が私たちから離れていく速度を表すものです。そして、それは間接的に宇宙が拡がる率を示しています。図9はこの方程式の基になったデータです。
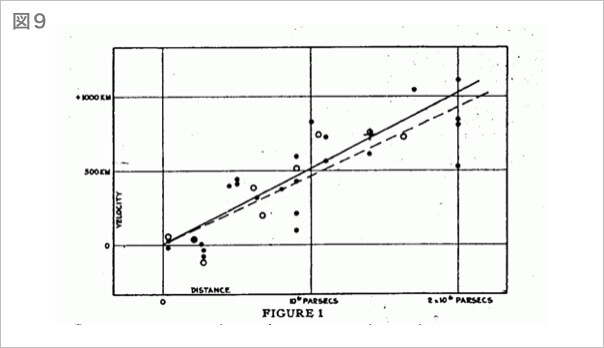
「Hubbleが天才的だったのは、このデータを見て、直線を引くことを思いついたことだ」と言われます。
グラフ上の点に合わせるために、もっと複雑な曲線を描くことも考えられたはずです。その場合、宇宙が拡がる率は場所によって速かったり遅かったりして予測不可能だということになります。
Wilks式でも同じようなことが起きているのだと考えられます。Wilks式は基になったデータには忠実ですが、データに忠実であることを優先して複雑になり、本来見るべき筋力と体重の関連性を捉えられていない可能性が高いということです。
Wilks式を開発する目的が、挙上成績を各階級ごとにスコア化して、そのスコア比較でのベストリフターを決めることであれば、Wilks式の開発に用いられたアプローチは悪くないと言えます。しかし、Wilks式の目的が、本当の意味で最も大きな相対重量を挙げたベストリフターは誰かを特定し、階級のちがう選手間で正確に相対重量の比較を行うための尺度を作ることであれば、Wilks式が非常に複雑にできていることを見ると、目的に合った方程式ではないと考えられます。
実際のところ、中量級の選手層の厚さを考えると、大多数の競技大会においてベストリフターは中量級の選手になるはずです。
新しい記録が反映されない
Wilks式は1994年に導入されてから変更されていません。
1987〜1992年の間に、パワーリフティングの絶対的な限界になるパフォーマンスが出ていて、各階級の競技人口のバランスも当時からまったく変わらないとすれば、Wilks式に変更は必要ないのですが、どちらも現実に即しているとは言えません。
一方、ウェイトリフティングで用いられるSinclair式は、4年ごとに過去4年間のトップパフォーマンスを反映して更新されます。相対成長スケーリングのように、ヒトの身体にある基本的な関連性を用いた方法ではなく、競技成績のデータに基づいた尺度で相対重量を評価するのであれば、方程式は最新のデータを基にするべきです。特にパワーリフティングは競技人口が大きく伸びているので、このことは重要になります。
トータルの挙上重量に基づいている
Wilks式はトータル挙上重量の記録に基づいています。パワーリフティングの大会でベストリフターを決める際には、これは弱点になるというわけではありませんが、各種目ごとの相対重量を比較したいと思う人は少なくありません。Wilks式はベンチプレスの相対重量の比較にも使えることが示されていますが、各種目の挙上重量を比較することに特化した方法があるとベターでしょう。
どうすれば良いのか?
Wilks式に変わる相対重量の比較方法を2通り考えました。
方法1:相対成長スケーリングスコア
相対成長スケーリングのスコアを基に、各選手の挙上重量を比較するのはシンプルです。比較したい大会や競技形式での最高記録を100として、相対成長スケーリングのスコア(挙上重量×体重-2/3)の値で割ると係数が得られます。
例えば、IPFのノーギアのスクワットは係数が6.487682129になります。これに相対成長スケーリングのスコア(約15.41)を掛けると100になるということです。他の挙上記録では、相対成長スケーリングのスコアが15.41以下になるので、そのスコアに係数を掛けると、最高記録の100を基準とした比較ができます。
すでに話したように、相対成長スケーリングは生物学的に見たヒトの身体という理論と、実際の挙上重量という現実の世界が重なる理想的な方法です。
方法2:実際の競技大会のデータを分析する
実際の競技大会の挙上記録をシンプルな方法で分析して相対重量の比較をすることもできます。名付けて「Nuckols Index」です。
この記事の前半で選手の体重が大きくなるにつれて、体重に対する相対的な挙上重量は下がっていくことを紹介しました。この相対重量の下がり方を分析してみると、直線的であること分かります。
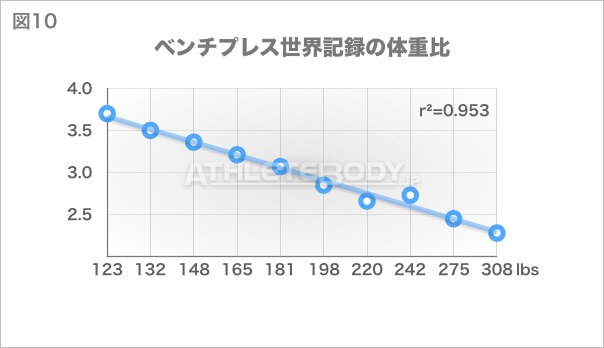
具体例を見てみましょう。まず、図10はドーピングテストの無いベンチプレスの体重と世界記録の関係です。
次は、IPFの合計挙上重量の世界記録です。
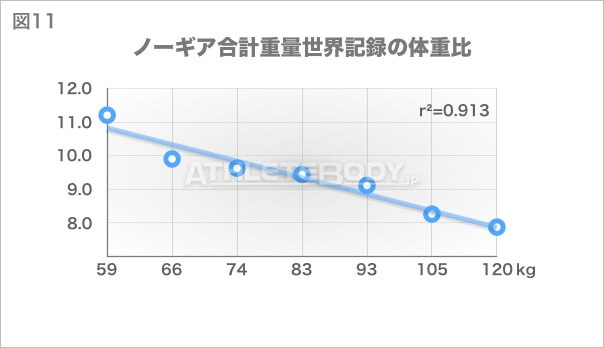
r²は、ほとんどのケースで+0.9以上と全体に非常に高い値になります。例外として挙げられるのがStanaszek選手で、彼の記録の入るデータではr²が0.72になります。そのデータから彼の記録だけ取り除くと、r²は約0.85まで上がります。(彼ほどの特別なケースでは、除外して分析することは完全に正当だと言えます。)女性の挙上記録では、ここまでハッキリと関連性が表れないのですが、これは競技人口が少ないことが影響しているはずです。これから女性選手が増えると、関連性が見えてくると考えて大丈夫でしょう。
これらのグラフから、体重制限のある階級の相対重量を比較する方程式を作るのは比較的簡単でした。ドーピングテストのない世界記録では308lbs級まで、IPFの世界記録では120kg級までが対象になります。
この方程式は「100*w/(a*bw2+b*bw) 」という形になります。少し複雑に見えるかもしれませんが、Wilks式は「100*w/(a+b*bw+c*bw2+d*bw3+e*bw4+f*bw5) 」になることを考えると、ずっとスッキリしていると言えるでしょう。
- w=各種目での挙上重量
- bw=体重
- aとbは各種目ごとの係数です。
Wilks式と比べてこの方程式には4つの強みがあります。
- まず、この方程式は2次の多項式で、5次の多項式であるWilks式よりもずっとシンプルです。これは、体重と挙上重量の間にある本当の関連性をWilks式よりもうまく捉えられている可能性が高いはずだと言えます。係数が少なくシンプルになることで、扱いやすくなることも強みです。
- 記録が更新されるのに合わせて方程式を更新することも比較的簡単で、Wilks式のように時代に取り残されることがありません。
- この方程式は世界記録のみを反映しているので、階級ごとの選手層の厚みの違いの影響を大きく減らすことができます。どこかの時点で力のある選手が打ち立てた世界記録のみを考慮し、さらに力のある選手によって記録が更新されれば、その新しい記録を反映します。方程式の基になる記録の数が少ないことが弱点とも言えますが、階級ごとに選手層の厚みが違うことで階級をまたいだ比較ができなくなる問題は緩和されます。実際にこの方法では、特定の体重の範囲や特定の階級に対して、ハッキリと有利に働いたり不利に働いているということは見られません。ドーピングテスト無しの記録をこの方程式でスコア化すると、スクワット、ベンチプレス、デッドリフト、3種目合計それぞれのトップ3のスコアに123lbs級で2つ、132lbs級で1つ、198lbs級で2つ、220lbs級で2つ、242lbs級で1つ、275lbs級で2つ、308lbs級で2つの記録が入りました。IPFの世界記録をスコア化すると、59kg級で3つ、66kg級で1つ、74kg級で2つ、93kg級で3つ、120kg級で2つがトップ3に入りました。
- この方程式では、3種目の合計挙上重量だけでなく、各種目の挙上重量も階級をまたいで比較することができます。
この方程式をIPFの世界記録に当てはめると以下のようになります。
| 表4:Nuckols Indexで見る世界記録 | ||||||||
|---|---|---|---|---|---|---|---|---|
| 階級 | スクワット | ベンチプレス | デッドリフト | 合計 | ||||
| 重量 | スコア | 重量 | スコア | 重量 | スコア | 重量 | スコア | |
| 59 | 226 | 98.23 | 170 | 92.59 | 270.5 | 94.35 | 661 | 100 |
| 66 | 240.5 | 95.48 | 182.5 | 92.37 | 278 | 89.55 | 653.5 | 90.80 |
| 74 | 260 | 94.52 | 210.5 | 100 | 310.5 | 93.40 | 712.5 | 91.77 |
| 83 | 280.5 | 93.75 | 205 | 91.26 | 316 | 88.84 | 783.5 | 94.19 |
| 93 | 303 | 93.67 | 232.5 | 99.04 | 372.5 | 100 | 847.5 | 95.87 |
| 105 | 330 | 94.54 | 221.5 | 90.41 | 343 | 87.22 | 867.5 | 92.68 |
| 120 | 375 | 100 | 235 | 94.49 | 37.15 | 92.13 | 945 | 96.81 |
| 重量単位:kg | ||||||||
次にドーピングテストの無い世界記録です。
| 表5:Nuckols Indexで見る世界記録(ニーラップ有り) | ||||||||
|---|---|---|---|---|---|---|---|---|
| 階級 | スクワット | ベンチプレス | デッドリフト | 合計 | ||||
| 重量 | スコア | 重量 | スコア | 重量 | スコア | 重量 | スコア | |
| 123 | 639 | 100 | 455 | 100 | 634 | 97.56 | 1339 | 93.87 |
| 132 | 565 | 81.51 | 4.62 | 96.26 | 628 | 91.49 | 1471 | 97.58 |
| 148 | 611 | 80.49 | 498 | 95.77 | 697 | 94.17 | 1581 | 95.85 |
| 165 | 710 | 87.10 | 529 | 94.73 | 717 | 90.26 | 1714 | 95.79 |
| 181 | 744 | 85.21 | 556 | 94.17 | 791 | 94.80 | 1840 | 96.28 |
| 198 | 810 | 87.59 | 565 | 91.00 | 870 | 100 | 2028 | 100 |
| 220 | 915 | 93.27 | 586 | 89.74 | 901 | 98.97 | 2110 | 97.23 |
| 242 | 881 | 83.91 | 661 | 98.00 | 893 | 94.85 | 2210 | 96.35 |
| 275 | 992 | 89.31 | 675 | 96.84 | 906 | 94.04 | 2380 | 97.35 |
| 308 | 1030 | 88.53 | 701 | 99.92 | 939 | 98.19 | 2425 | 94.68 |
| 重量単位:lbs | ||||||||
この方程式は、挙上重量と体重の比率が基になっており、体重が大きくなるに従って、体重に対する相対重量は直線的に下がっていくという関連性を利用しています。ここまでに紹介したドーピングテスト無しの308lbs級やIPF120kg級までは、大きな問題なく使えることが分かります。
しかし、体重300kgの選手がいたらどうなるかといったことを試すと、おかしなことが起こります。ドーピングテストの無い大会で600lbsのスクワット、もしくはIPFで260kgのスクワットでスコアが100を超えるという数字が出てしまうのです。これは、体重に対する挙上重量の比率が1以下になってしまうことから来ています。
この問題には、体重制限のない階級には、相対成長スケーリングを使うことで対応できます。308lbs級と120kg級でNuckols Indexのスコアが100になる挙上記録と、その相対成長スケーリングスコアを使います。
どちらの方法が良いかと言うと、私個人の意見では、Nuckols Indexよりも相対成長スケーリングのスコアの方が良いと思います。実際の競技大会の成績を基にした方法でないと納得がいかないと考えるなら、Nuckols IndexはWilks式よりも優秀なはずです。ただ、体重制限のない階級には相対成長スケーリングを使う形になりますし、相対成長スケーリングは理論的にしっかりしていることが強みです。
ただ、どちらの方法を使っても、体重制限のない最重量級は相対筋力の比較をする限りさみしい数字しか出ないという事実があります。これに関しては、そうあるべきだと言うことでしょう。
そもそも、パワーリフティングは相対筋力を競うスポーツであり、ベストリフター賞は最も大きな相対重量を挙げた選手におくられるべきものです。ここまで読んでくれた人には、相対筋力の比較というのは、挙上重量を体重で割るだけというほどシンプルな話でないことは伝わったと思います。しかし、相対筋力を考えるときの根本的な原則として、体脂肪が大きく違わず(5〜10%以内程度の差)、挙上スキルが同レベルにある人を比較すると、概ね同程度の相対筋力を発揮できることになるということです。
体重制限のある階級のトップ選手と比べると、最重量級の選手は全般的にかなり体脂肪が多くなります。相対成長スケーリングのスコアで比較すると、最重量級の世界記録保持者の中では最も体重の軽い選手でやっと他の階級の選手と肩を並べられるくらいでした。つまり、体重制限のない最重量級は絶対重量で勝負するスポーツだということでしょう。もし、最重量級の選手が相対筋力で勝負したいと考えるなら、Wilks式のような方程式の助けを借りて優位に立つのではなく、他の階級のトップ選手と同じレベルまで体脂肪を落とすべきだということです。
まとめ
相対筋力を平等に比較するには、挙上重量を体重で割った数字のようなシンプルな方法ではまったく不十分だということです。
体重と挙上重量の間にある関連性から、相対成長スケーリングが相対筋力を比較するのに理想的な方法となります。理論的にも支持されていて、現実の世界でも妥当性が確認できています。
パワーリフティングで使われるWilks式は、中量級の選手に不利に働き、軽量級、重量級の選手に有利に働くようにできています。Wilks式のような実際の挙上記録を基にした方程式を使うのであれば、少なくとも定期的に新しい記録を反映することが必要です。
相対重量を比較するには、相対成長スケーリングのスコアを使っても良いですし、Nuckols Indexを使っても良いでしょう。しかし、挙上重量/体重の比率や、Wilks式には大きな欠陥があり、新しい方法に置き換わるべきです。
相対重量を平等に比較できる方法を使うと、体重制限のない最重量級の選手の挙上記録は、相対重量としての評価が低く出ます。体脂肪が多いことで体重が重くなれば、相対筋力は低くなるものなので、それが反映されるのは良いことでしょう。絶対重量が大きいことと相対重量としての評価は別です。最重量級の選手が相対重量でも勝負したいと思うなら、体重制限のある階級の選手達と同程度のレベルまで体脂肪を落とすべきです。そうでなければ、最重量級はもともと絶対重量の勝負の場なので、絶対重量に専念して、相対重量は他の階級に任せるべきでしょう。これは個人の価値観の問題にもなってきますが、Wilks式が最重量級の選手にどれだけ有利に働くかを考えると、相対重量を平等に比較しているとは言えません。相対成長スケーリングを基準に、体重150kgの選手と72.5kgの選手を比較すると、Wilks式では150kgの選手はWilksスコアが23%も高く出ることになります。さらに、体重180kgの選手になれば35%も大きくなるのです。
相対筋力を平等に比較するのは難しく、この記事に紹介したように相対成長スケーリングを使ったスコア化や、パワーリフティングの場合には、実際の競技成績を基にした方程式など複数の方法が考えられます。AthleteBody.jpでは、相対成長スケーリングを用いて、身長と体重から挙上成績の相対重量を算出できる計算機を紹介しています。ご自身の数字が気になる方はこちらの記事をご覧ください。
- オリジナル記事
- 翻訳・編集:八百 健吾